A gentle introduction to GEMM using MMA tensor cores
There are a lot of resources online about writing a fast GEMM, and they all get complicated really fast, and by the time you reach the tensor core section you need to keep a lot in context to understand.
This post tries to go in reverse, using a tensor core on the smallest possible tile and build up from there. It's aimed at software developers who are interested in learning about tensor cores but haven't grokked the intricacies of a performant GEMM yet.
Background
Tensor cores are dedicated pieces of hardware on a GPU that are part of a Shared Multiprocessor (SM). They are blazingly fast, and keeping their throughput high is a big challenge.
The only prior knowledge this post assumes is about the CUDA programming model, and the matrix-multiplication operation.
For more background on tensor cores on CUDA, I refer you to this excellent article.
All the code used in this article is available here
MMA Cores
MMA instructions work at a warp-level, i.e. 32 threads in a warp conspire together to compute one small GEMM. In NVIDIA consumer GPUs, these are fastest options available, while for data-center cards multiple warps can be used to execute a bigger GEMM.
Note: There is also a higher level wmma instruction set which has a simpler API. However, it is not as feature dense (for example, it does not give you a well-defined memory layout) instead we focus on mma.
For this post we will choose the following instruction as our base:
mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32
Let's break it down. Just for reference, here is the GEMM operation:
m16n8k16 - m is 16, n is 8 and k is 16. So the matrices A and B are 16 x 16 and 16 x 8
row - matrix A is in row-major format
col - matrix B is in col-major format
f32 - D's type
f16 - A's type
f16 - B's type
f32 - C's type
The official documentation is where we will get all our information about this instruction.
For the A matrix, this is how the threads should load their data in fragments:
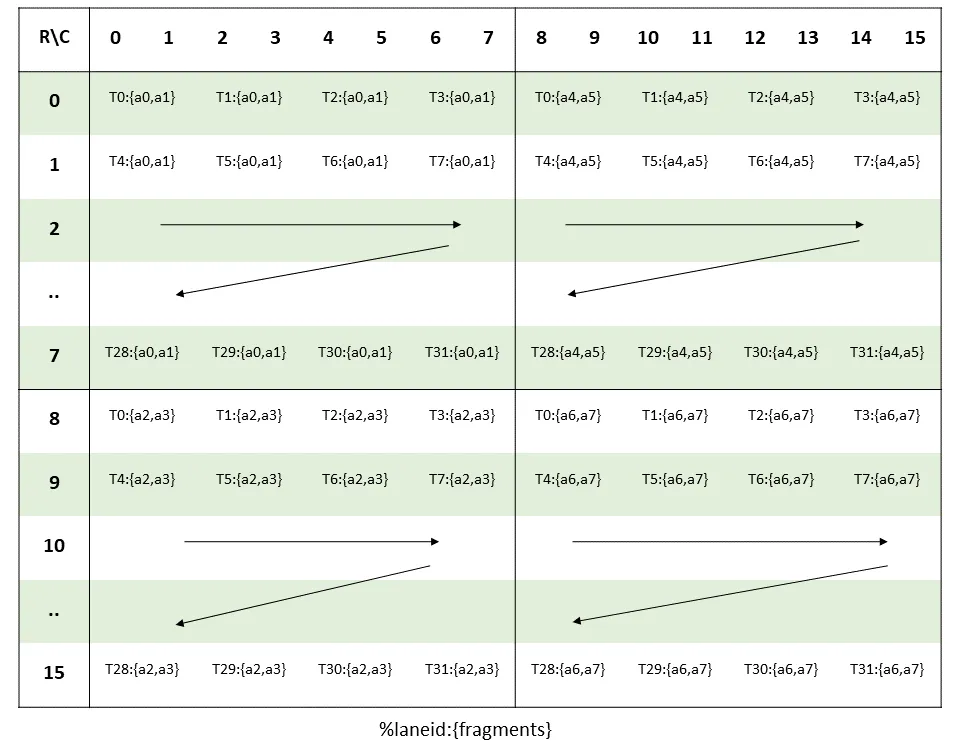
For example thread 1 in the diagram needs to hold:
Row 0 Col 2, Col 3: {a0, a1}
Row 8 Col 2, Col 3: {a2, a3}
Row 0 Col 10, 11: {a4, a5}
Row 8 Col 10, 11: {a6, a7}
Note that {a0, a1} means it needs to be a single 32 bit value, in our case it is 2 16-bit floats packed together.
The documentation also provides how to map each thread's loaded values:
groupID = %laneid >> 2
threadID_in_group = %laneid % 4
row = groupID for ai where 0 <= i < 2 || 4 <= i < 6
groupID + 8 Otherwise
col = (threadID_in_group * 2) + (i & 0x1) for ai where i < 4
(threadID_in_group * 2) + (i & 0x1) + 8 for ai where i >= 4
Let's create a helper function for loading the A fragment and add helper functions get_row and get_col given a laneid and an index. You can verify the get_row and get_col is the same as the one given in the PTX documentation, just without branches
template <typename T> struct Afrag_16x16 {
static constexpr size_t ne = 8; // num of elements per thread
T x[ne];
static __device__ size_t get_row(int tid, int l) {
int group_id = tid >> 2;
return group_id + 8 * ((l / 2) % 2);
}
static __device__ size_t get_col(int tid, int l) {
return 2 * (tid % 4) + (l % 2) + 8 * (l / 4);
}
};
Similarly for B (16 x 8 col-major matrix), we have
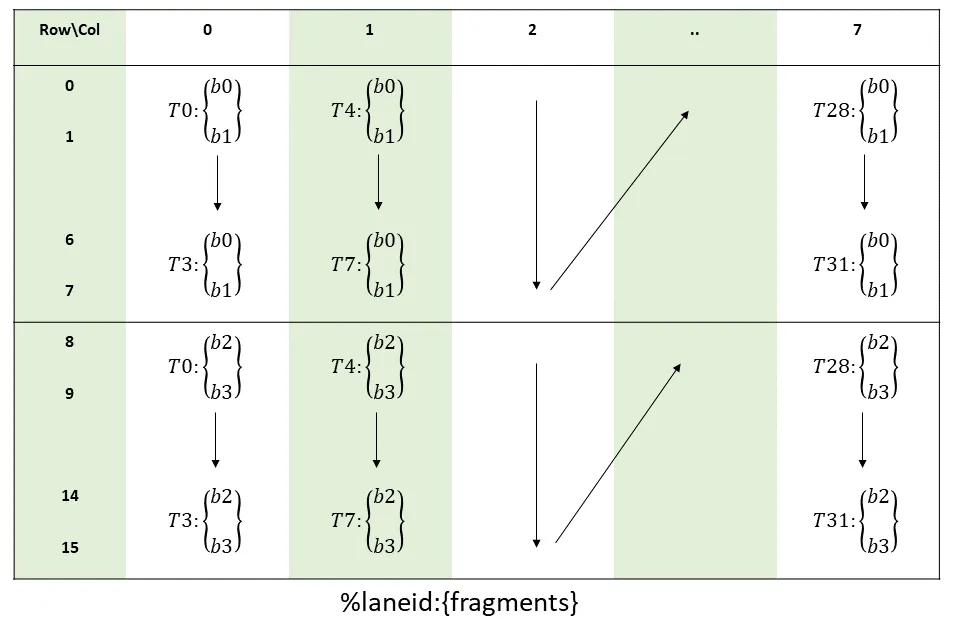
We'll create another helper function:
template <typename T> struct Bfrag_16x8 {
static constexpr size_t ne = 4;
T x[ne] = {};
static __device__ size_t get_row(int tid, int l) {
return (tid % 4) * 2 + (l % 2) + 8 * (l / 2);
}
static __device__ size_t get_col(int tid, int l) { return tid >> 2; }
};
And finally for C
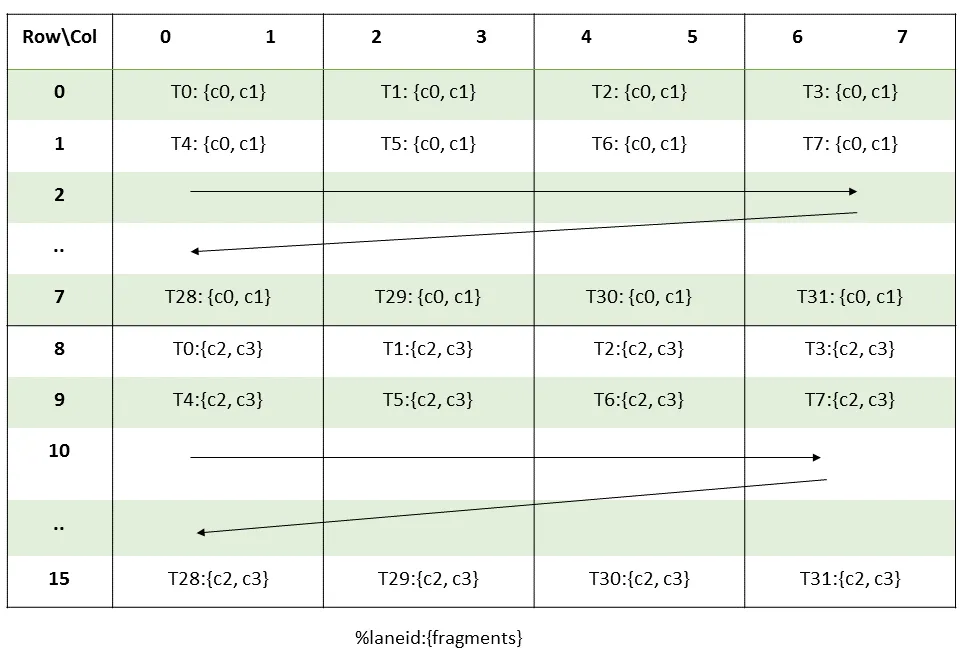
template <typename T> struct CFrag_16x8 {
static constexpr size_t ne = 4;
T x[ne] = {};
static __device__ size_t get_row(int tid, int l) {
return (tid >> 2) + 8 * (l / 2);
}
static __device__ size_t get_col(int tid, int l) {
assert(l < ne);
return 2 * (tid % 4) + (l % 2);
}
};
Notice that thread-mapping for B is the transpose for C
Microkernel
At this point, we are ready to call this instruction!
Our simple kernel looks like this. We can see the compiled PTX on godbolt
__global__ void mmaKernel(const half *A, const half *B, float *C, int M, int N,
int K) {
//Each thread has a copy of this tile
Afrag_16x16<half> a_tile;
Bfrag_16x8<half> b_tile;
CFrag_16x8<float> c_tile;
const int tid = threadIdx.x;
//Load A & B fragments
for (int idx = 0; idx < a_tile.ne; ++idx) {
a_tile.x[idx] = A[a_tile.get_row(tid, idx) * K + a_tile.get_col(tid, idx)];
}
for (int idx = 0; idx < b_tile.ne; ++idx) {
b_tile.x[idx] = B[b_tile.get_row(tid, idx) * N + b_tile.get_col(tid, idx)];
}
// mma instruction expects 32-bit int registers, we cast
const int *a_regs = (const int *)a_tile.x;
const int *b_regs = (const int *)b_tile.x;
asm volatile("mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32 "
"{%0, %1, %2, %3}, "
"{%4, %5, %6, %7}, "
"{%8, %9}, "
"{%0, %1, %2, %3};\n"
: "+f"(c_tile.x[0]), "+f"(c_tile.x[1]), "+f"(c_tile.x[2]),
"+f"(c_tile.x[3])
: "r"(a_regs[0]), "r"(a_regs[1]), "r"(a_regs[2]), "r"(a_regs[3]),
"r"(b_regs[0]), "r"(b_regs[1]));
//3. Write back to C
for (int i = 0; i < c_tile.ne; ++i) {
int row = c_tile.get_row(tid, i);
int col = c_tile.get_col(tid, i);
C[row * N + col] = c_tile.x[i];
}
}
This kernel works, but only for M=16, N=8, K=16. It was cumbersome to get the right layout though, and our data loads are scattered which is not good for performance. This is where ldmatrix comes in.
Using ldmatrix
ldmatrix is an instruction which simplifies loading matrix fragments into registers from shared memory, while being faster.
We can think of ldmatrix as a function from raw row-major matrices living in shared memory to the matrix fragments living in registers mma expects.
The ldmatrix instruction will only load matrix fragments from shared memory. For our use case of 16-bits inputs, ldmatrix loads matrices in a 8x8 tile.
Let's dissect the instruction we're going to be using for A
ldmatrix.sync.aligned.m8n8.x4.shared.b16
ldmatrix.sync.aligned - mandatory arguments
m8n8 - only available configuration for 16-bit input
x4 - we can either do 1, 2, 4 tile loads. For 16x16 we need to use 4
shared - load from shared memory
b16 - the output format, also 16 bit for us
This is how the tiles look in memory (each is of size 8x8 16-bit elements)
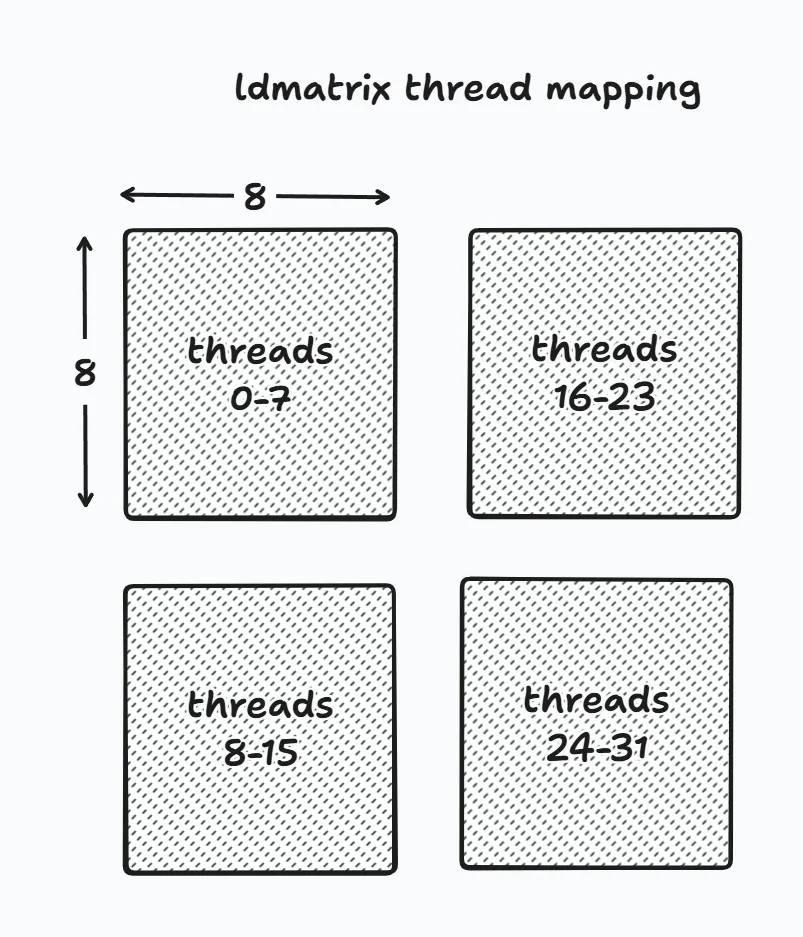
The way for a thread to get its starting row/col is then:
row = threadIdx.x%16
col = (threadIdx/16)*8
For B we can reload x1 and x2 at x3 and x4 respectively, as it allowed in the documentation.
addresses contained in lower threads can be copied to higher threads to achieve the expected behavior.
So for B, we use
row = threadIdx.x % 16
col = 0
We also use ldmatrix.sync.aligned.m8n8.x2.shared.trans.b16 as we want to load B in a column-major format.
Micro-kernel with ldmatrix
Our new and improved kernel, which has better memory-coalescing looks like this. Here is the godbolt link
__global__ void mmaKernel(const half *A, const half *B, float *C, int M, int N,
int K) {
Afrag_16x16<half> a_tile;
Bfrag_16x8<half> b_tile;
CFrag_16x8<float> c_tile;
const int tid = threadIdx.x;
__shared__ alignas(16) half A_shared[16][16];
__shared__ alignas(16) half B_shared[16][8];
const int lane = tid & 31;
// Use 16 threads to load shared mem.
if (lane < 16) {
int row = lane;
for(int idx = 0; idx < 8; ++idx) {
A_shared[row][idx] = A[row*K + idx];
}
for(int idx = 0; idx < 8; ++idx) {
A_shared[row][idx + 8] = A[row*K + 8 + idx];
}
for(int idx = 0 ; idx < 8; ++idx) {
B_shared[row][idx] = B[row*N + idx];
}
}
int *a_regs = (int *)a_tile.x;
int *b_regs = (int *)b_tile.x;
int lane_id = tid;
uint32_t a_addr = __cvta_generic_to_shared(
&A_shared[(lane_id % 16)][(lane_id / 16) * 8]);
uint32_t b_addr = __cvta_generic_to_shared(
&B_shared[(lane_id % 16)]);
asm volatile("ldmatrix.sync.aligned.m8n8.x4.shared.b16 "
"{%0, %1, %2, %3}, [%4];"
: "=r"(a_regs[0]), "=r"(a_regs[1]), "=r"(a_regs[2]),
"=r"(a_regs[3])
: "r"(a_addr));
asm volatile("ldmatrix.sync.aligned.m8n8.x2.shared.trans.b16 "
"{%0, %1}, [%2];"
: "=r"(b_regs[0]), "=r"(b_regs[1])
: "r"(b_addr));
asm volatile("mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32 "
"{%0, %1, %2, %3}, "
"{%4, %5, %6, %7}, "
"{%8, %9}, "
"{%0, %1, %2, %3};\n"
: "+f"(c_tile.x[0]), "+f"(c_tile.x[1]), "+f"(c_tile.x[2]),
"+f"(c_tile.x[3])
: "r"(a_regs[0]), "r"(a_regs[1]), "r"(a_regs[2]), "r"(a_regs[3]),
"r"(b_regs[0]), "r"(b_regs[1]));
for (int i = 0; i < c_tile.ne; ++i) {
int row = c_tile.get_row(tid, i);
int col = c_tile.get_col(tid, i);
C[row * N + col] = c_tile.x[i];
}
}
A couple of things to note:
- Why
alignas(16)on shared memory -ldmatrixmandates 16-byte aligned rows. This is because a group of 4 threads load 16 bytes (1 row in our case 2 bytes of f16 x 8) at once. __cvta_generic_to_shared- this is just a way to convert a raw pointer to a pointer to shared memory- All optimizations like avoiding bank conflicts, vectorized gmem/smem loads are left for later
- We don't need a
__syncthreads()because the block is a single warp
There is also stmatrix, which goes the opposite way as ldmatrix and would be useful for storing C, but that is only available post sm_90(Hopper and beyond) and I don't have a GPU handy for that.
Full GEMM
Now that we our tile, we still don't know how to calculate the full GEMM. However, we can easily solve for any M (divisible by 16) and N (divisible by 8) as long as we keep K = 16. We can just launch more blocks, each calculating a tile. This is easier because we don't have to accumulate partial sums for K.
This post wouldn't be complete without a drawing of a matrix, so here it is:
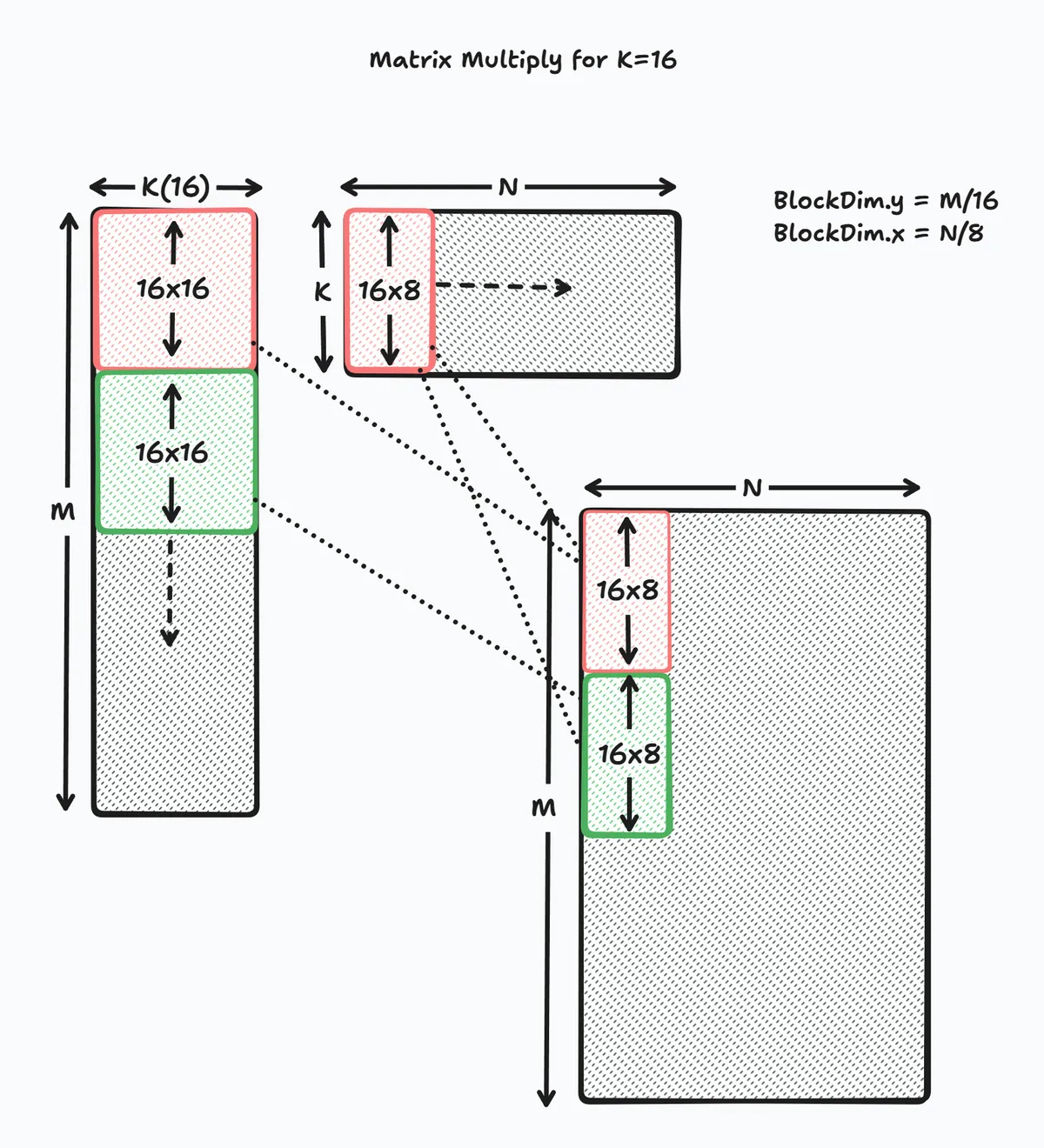
As is hopefully clear from the diagram, we need to make the following changes:
- Launch a 2-d grid of blocks (instead of 1),
N/8in the x-dimension andM/16in the y-dimension - Move A and B matrices to the correct offset
int c_row = blockIdx.y * 16;
int c_col = blockIdx.x * 8;
A += c_row * K;
B += c_col;
- Use
c_rowandc_colto move C to the correct position
for (int i = 0; i < c_tile.ne; ++i) {
int row = c_row + c_tile.get_row(tid, i);
int col = c_col + c_tile.get_col(tid, i);
C[row * N + col] = c_tile.x[i];
}
The next step is to handle the case where K is a multiple of 16, for this we break K down into K/16 pieces, and accumulate the results. Mathematically we are doing the following:
Here's a diagram
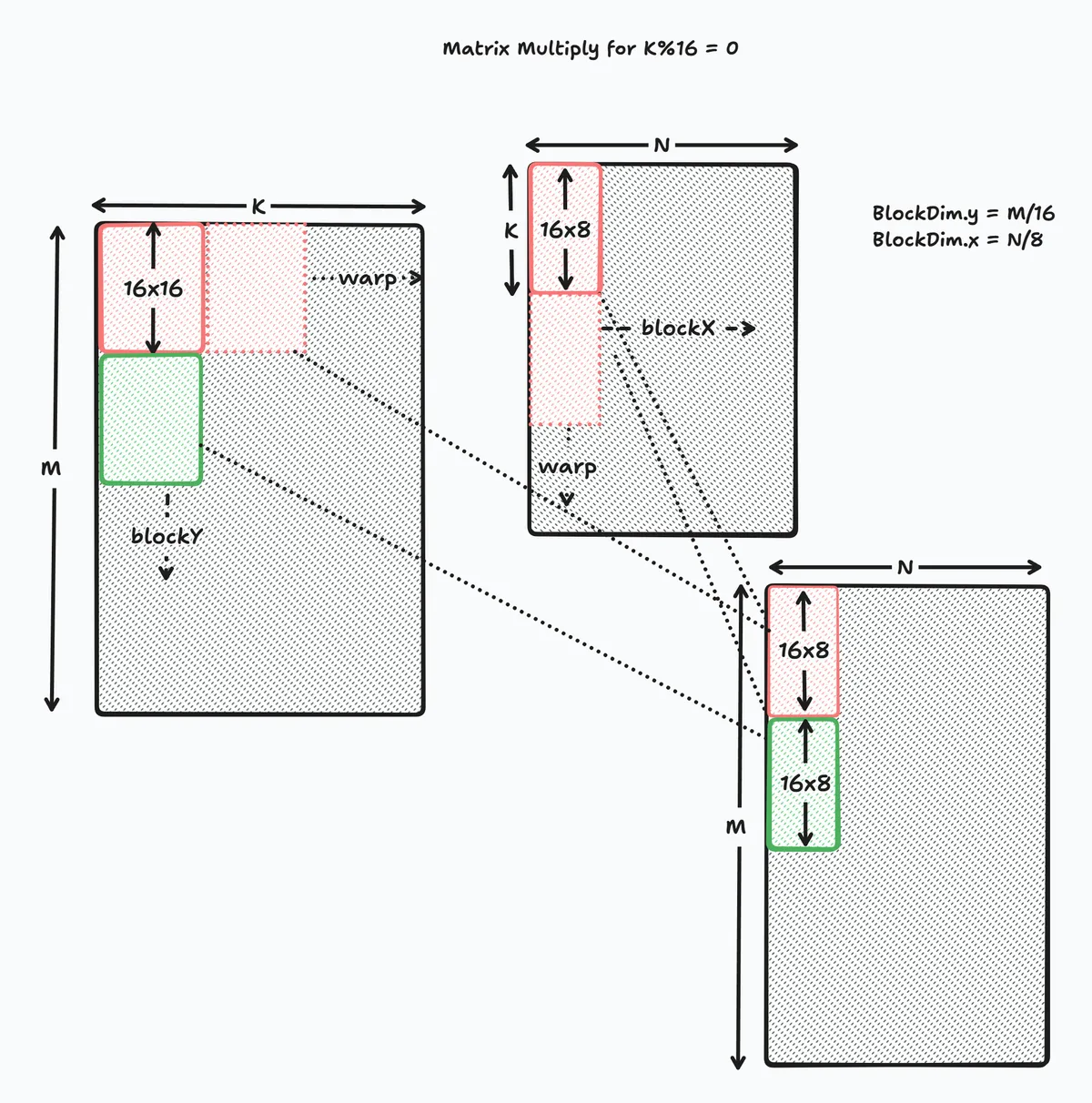
And the relevant code block
for(int k_idx = 0; k_idx < K; k_idx += 16) {
if (lane < 16) {
int row = lane;
for(int idx = 0; idx < 8; ++idx) {
A_shared[row][idx] = A[row*K + idx];
}
for(int idx = 0; idx < 8; ++idx) {
A_shared[row][idx + 8] = A[row*K + 8 + idx];
}
for(int idx = 0 ; idx < 8; ++idx) {
B_shared[row][idx] = B[row*N + idx];
}
}
A += 16; //move A 16 columns ahead
B += 16*N; // move B 16 rows ahead
//same as before. c_tile keeps accumulating partial sums
}
for (int i = 0; i < c_tile.ne; ++i) {
int row = c_row + c_tile.get_row(tid, i);
int col = c_col + c_tile.get_col(tid, i);
C[row * N + col] = c_tile.x[i];
}
There you have it, a completely functioning (albeit slow) GEMM using tensor cores! Here is the godbolt link.
Let's benchmark this kernel against gold-standard cuBLAS. On my 3090,
=== GEMM Benchmark (M=1024, N=1024, K=32) ===
FLOPs: 0.067 GFLOPs
mmaKernel: 1.907 ms | 35.20 GFLOPs
cuBLAS: 0.286 ms | 234.90 GFLOPs
Speedup (cuBLAS / mma): 6.67x
So we are embarrassingly slow even for small K, which will only get worse as we increase our K.
Optimizing
Most optimizations from here follow the basic principle: data-movement is slow, and compute is fast. We need to exploit the memory hierarchy via data-reuse/data-locality/asynchronous data transfers.
There are many, excellent, articles which go into this topic in detail. Hopefully this post demystifies some of the PTX MMA semantics.